Nilai Puncak, Nilai Rata-rata dan Nilai RMS
Seperti yang Anda ketahui, bentuk gelombang AC bersifat sinusoidal. Besarnya terus bervariasi dengan waktu, maka perlu untuk menemukan nilai pada setiap instan dan nilai puncaknya.
Mirip dengan DC, yang memiliki besarnya konstan, kita menemukan nilai rata -rata kuantitas AC, yang juga akan memiliki besarnya konstan. Untuk satu siklus lengkap, Anda mendapatkan nol sebagai nilai rata -rata karena memiliki siklus positif dan negatif.
Nilai Puncak (Peak Value)
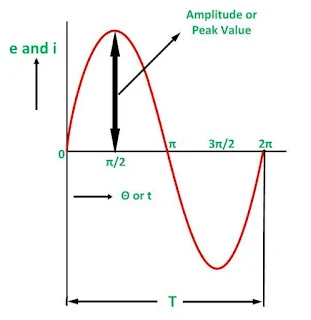
Nilai maksimum yang dicapai oleh kuantitas bergantian selama satu siklus disebut nilai puncaknya. Ini juga dikenal sebagai nilai maksimum atau amplitudo atau nilai puncak. Kuantitas bolak -balik sinusoidal memperoleh nilai puncaknya pada 90 derajat seperti yang ditunjukkan pada gambar di bawah ini.
Nilai puncak tegangan dan arus bolak -balik diwakili masing -masing oleh Em dan Im.
Nilai Rata-rata (Average Value)
Definisi: Rata -rata semua nilai sesaat dari tegangan bergantian dan arus selama satu siklus lengkap disebut nilai rata -rata.
Jika kita mempertimbangkan gelombang simetris seperti arus sinusoidal atau bentuk gelombang tegangan, setengah siklus positif akan persis sama dengan setengah siklus negatif. Oleh karena itu, nilai rata -rata selama siklus lengkap akan menjadi nol.
Pekerjaan dilakukan oleh keduanya, siklus positif dan negatif dan karenanya nilai rata -rata ditentukan tanpa mempertimbangkan tanda -tanda.
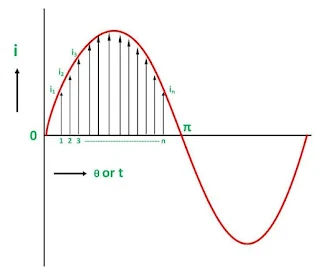
Bagilah setengah siklus positif menjadi (n) jumlah bagian yang sama seperti yang ditunjukkan pada gambar di atas.
Dimana i1, i2, i3…….. in ditengah ordinat
Nilai rata -rata Iav saat ini = rata -rata dari ordinat tengah
Nilai R.M.S.
Definisi: Arus mantap yang, ketika mengalir melalui resistor resistensi yang diketahui untuk periode waktu tertentu daripada sebagai hasilnya jumlah panas yang sama dihasilkan oleh arus bolak -balik ketika mengalir melalui resistor yang sama untuk periode waktu yang sama dipanggil disebut R.M.S atau nilai efektif dari arus bolak -balik.
Dengan kata lain, nilai R.M.S didefinisikan sebagai akar kuadrat dari sarana kuadrat dari nilai -nilai instan.
Biarkan saya menjadi arus bolak -balik yang mengalir melalui resistor r untuk waktu t detik, yang menghasilkan jumlah panas yang sama seperti yang dihasilkan oleh arus searah (Ieff). Basis satu perubahan dibagi menjadi N bagian yang sama sehingga setiap interval adalah t/n detik seperti yang ditunjukkan pada gambar di bawah ini.
Biarkan i1, i2, i3, ……… ..Dalam ordinat tengah
Kemudian panas yang dihasilkan
Karena Ieff dianggap sebagai nilai efektif dari arus ini, maka total panas yang dihasilkan oleh arus ini akan
Sekarang, menyamakan persamaan (1) dan (2) yang akan kita dapatkan
Ieff = akar kuadrat rata -rata kotak nilai instan = nilai r.m.s
Root mean square adalah nilai aktual dari kuantitas bergantian yang memberi tahu kita kemampuan transfer energi dari sumber AC.
Ammeter mencatat nilai RMS dari nilai arus bolak -balik dan voltmeter dari nilai root mean square (r.m.s) dari tegangan bergantian. Pasokan AC fase tunggal domestik adalah 230 V, 50 Hertz, di mana 230 V adalah nilai R.M.S dari tegangan bergantian.
Nilai tegangan dan sistem saat ini dalam sirkuit DC konstan, jadi tidak ada masalah dalam mengevaluasi besaran mereka, tetapi dalam sistem AC, tegangan bergantian dan arus bervariasi dari waktu ke waktu dan karenanya perlu mengevaluasi besaran mereka .
Tiga cara berikut (nilai puncak, nilai rata -rata dan nilai r.m.s) yang diberikan di atas diadopsi untuk mengekspresikan besarnya tegangan dan arus.
